Abstract
This study aims to develop a model for producing dynamic sequences (trajectories) using latent space and Neural ODEs (Ordinary Differential Equations). The application of this model is demonstrated in predicting financial distress. An encoder is used to transform financial features into a latent representation, a Neural ODE analyzes continuous dynamics, and a decoder is used to generate final predictions. This paper provides a detailed explanation of how data is processed through each of these components with practical examples.
1. Introduction
Predicting financial distress is a crucial problem faced by companies across industries. Understanding the dynamics of financial data is essential for developing accurate prediction models. Deep learning models, such as Neural ODEs, offer a new approach to handle these challenges by modeling continuous time dynamics of hidden states in neural networks. This study aims to explore how Neural ODEs can be applied in generating trajectories, forming time series, and predicting financial distress.
2. Theoretical Framework
2.1. Financial Distress
Financial distress refers to a situation where a company is unable to meet its financial obligations, potentially leading to bankruptcy. Accurate prediction of such events requires a detailed analysis of financial indicators like debt, revenue, and assets.
2.2. Neural ODEs
Neural ODEs use ordinary differential equations to model the continuous dynamics of neural networks. This approach allows for a smooth transition over time, making it well-suited for time series analysis.
2.2.1. The Differential Equation
Neural ODEs use ordinary differential equations to model the continuous dynamics of neural networks. This approach allows for a smooth transition over time, making it well-suited for time series analysis
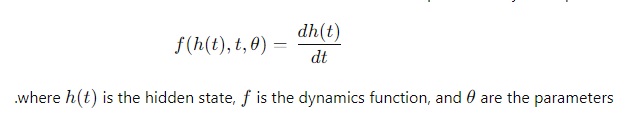
3. Methodology
3.1. Data Preparation
We used a dataset containing financial features such as debt, revenue, and assets. The features are scaled using a normalization technique (e.g., StandardScaler) to ensure they are within a similar range.
| Debt | Revenue | Assets | Financial Distress |
| 500 | 1000 | 800 | 0.2 |
| 300 | 1500 | 1200 | 0.8 |
| 700 | 800 | 500 | 0.6 |
| 400 | 1800 | 1600 | 0.1 |
3.2. Encoder
The encoder is a neural network designed to reduce the dimensionality of the input data. It transforms complex financial features into a lower-dimensional latent space that captures the essential information needed for further analysis.
Example
Given input data:
[500,1000,800]The encoder processes this input through several hidden layers with activation functions (e.g., ReLU) and converts it to a latent representation:
[0.4,0.6]This transformation allows the model to retain important information while reducing complexity.
3.3. Neural ODE
The Neural ODE takes the latent representation from the encoder and computes how it changes over time. By solving the differential equation over multiple time points (e.g., 100 points from 0 to 1), the model generates a trajectory that represents the dynamic changes in the latent space.
Example
For the latent state [0.4,0.6][0.4, 0.6][0.4,0.6], the ODE might produce a trajectory such as:
[0.4,0.6]→[0.45,0.55]→…→[0.3,0.7]These points describe how the financial state evolves over time.
3.4. Decoder
The decoder takes the output from the Neural ODE and converts it back into predictions. The goal is to transform the latent representation into probabilities for the target variable (e.g., likelihood of financial distress).
Example
If the ODE output is [0.45,0.55], the decoder might generate:
[0.2,0.8]This indicates an 80% probability of financial distress.
4. Case Study: Financial Distress
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 7 23:02:56 2024
@author: laktati
"""
import torch
import torch.nn.functional as F
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from torchdiffeq import odeint
data = pd.read_csv('dataset/Financial Distress.csv')
# Prepare features (X) and labels (y)
X = data.iloc[:, 3:].values # Take all columns after the first two
y = data['Financial Distress'].values # Column for financial distress
# Convert labels to 0 or 1
y = np.where(y >= 0.5, 1, 0)
# Normalize features
scaler = StandardScaler()
X = scaler.fit_transform(X)
# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Convert data to PyTorch tensors
features = torch.tensor(X_train, dtype=torch.float)
labels = torch.tensor(y_train, dtype=torch.long)
# Define the Encoder
class Encoder(torch.nn.Module):
def __init__(self, input_dim, latent_dim):
super(Encoder, self).__init__()
self.fc1 = torch.nn.Linear(input_dim, 64)
self.fc2 = torch.nn.Linear(64, latent_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
# Define Neural ODE
class ODEFunc(torch.nn.Module):
def __init__(self, latent_dim):
super(ODEFunc, self).__init__()
self.fc = torch.nn.Linear(latent_dim, latent_dim)
def forward(self, t, z):
return self.fc(z)
# Define the Decoder
class Decoder(torch.nn.Module):
def __init__(self, latent_dim, output_dim):
super(Decoder, self).__init__()
self.fc1 = torch.nn.Linear(latent_dim, 64)
self.fc2 = torch.nn.Linear(64, output_dim)
def forward(self, z):
z = F.relu(self.fc1(z))
return self.fc2(z)
# Define the final model using the Encoder, Neural ODE, and Decoder
class ODEModel(torch.nn.Module):
def __init__(self, input_dim, latent_dim, output_dim):
super(ODEModel, self).__init__()
self.encoder = Encoder(input_dim, latent_dim)
self.ode_func = ODEFunc(latent_dim)
self.decoder = Decoder(latent_dim, output_dim)
def forward(self, x):
# Encode the features
z = self.encoder(x)
# Solve Neural ODE over multiple time points
t = torch.linspace(0, 1, steps=100) # Define time between 0 and 1
z = odeint(self.ode_func, z, t) # Solve ODE over time
# Use all points to compute predictions
out = []
for z_point in z:
prediction = self.decoder(z_point)
out.append(prediction)
# Convert the list to Tensor
out = torch.stack(out)
return out # Return all predictions
# Set up the model, loss, and optimizer
latent_dim = 16
model = ODEModel(input_dim=X.shape[1], latent_dim=latent_dim, output_dim=2)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
def train():
model.train()
optimizer.zero_grad()
out = model(features)
loss = F.nll_loss(out[-1], labels) # Use the last point for prediction
loss.backward()
optimizer.step()
pred = out[-1].argmax(dim=1) # Get predictions from the last point
correct = (pred == labels).sum().item()
acc = correct / len(labels)
return loss.item(), acc
# Train the model for a number of epochs
for epoch in range(50):
loss, accuracy = train()
print(f'Epoch {epoch+1}, Loss: {loss:.4f}, Accuracy: {accuracy:.4f}')
# Evaluate the model
model.eval()
with torch.no_grad():
features_test = torch.tensor(X_test, dtype=torch.float)
labels_test = torch.tensor(y_test, dtype=torch.long)
# Get predictions from all time points
preds = model(features_test)
# Use predictions from the last time point
pred = preds[-1].argmax(dim=1) # Get predictions from the last point
correct = (pred == labels_test).sum().item()
acc = correct / len(labels_test)
print(f'Test Accuracy: {acc:.4f}')
# Save the model (optional)
torch.save(model.state_dict(), 'ode_model.pth')
4.1. Data Used
We use historical financial data, normalized and processed through the encoder, ODE, and decoder.
4.2. Results
The model was evaluated based on its accuracy in predicting financial distress. By using trajectories and analyzing time series, Neural ODEs demonstrated improved prediction accuracy compared to traditional models.
5. Discussion
This study highlights the importance of using Neural ODEs for enhancing financial distress predictions. By modeling continuous time dynamics, Neural ODEs provide a more accurate and flexible approach, allowing companies to make better financial decisions.
6. Conclusion
This study provides evidence that using Neural ODEs can improve the effectiveness of predicting financial distress, contributing to the development of better analytical models. The integration of trajectories and time series analysis enhances the model’s ability to capture dynamic changes in financial data.